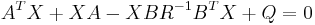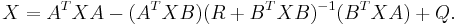Algebraic Riccati equation

The algebraic Riccati equation is either of the following matrix equations:

the continuous time algebraic Riccati equation (CARE):

$A^T X %2B X A - X B R^{-1} B^T X %2B Q = 0 \,$

or the discrete time algebraic Riccati equation (DARE):

$X = A^T X A -(A^T X B)(R %2B B^T X B)^{-1}(B^T X A) %2B Q.\,$

X is the unknown n by n symmetric matrix and A, B, Q, R are known real coefficient matrices.

The name Riccati is given to the CARE equation by analogy to the Riccati differential equation: the unknown appears linearly and in a quadratic term (but no higher-order terms). The DARE arises in place of the CARE when studying discrete time systems; it is not obviously related to the differential equation studied by Riccati.

The algebraic Riccati equation determines the solution of the infinite horizon time-invariant Linear-Quadratic Regulator problem (LQR) as well as that of the infinite horizon time-invariant Linear-Quadratic-Gaussian control problem (LQG). These are two of the most fundamental problems in control theory.

A solution to the algebraic Riccati equation can be obtained by matrix factorizations or by iterating on the Riccati equation.

References

Peter Lancaster; Leiba Rodman (1995), Algebraic Riccati equations, Oxford University Press, pp. 504, ISBN 0198537956

Alan J. Laub, A SCHUR METHOD FOR SOLVING ALGEBRAIC RICCATI EQUATIONS, http://dspace.mit.edu/bitstream/handle/1721.1/1301/R-0859-05666488.pdf;jsessionid=8CCF9A002524048AFD0F91D1F15EB6AE?sequence=1

Algebraic Riccati equation

See also

References

External links